The Law of Sines

The Law of Sines (or Sine Rule) is very useful for solving triangles:

a sin A = b sin B = c sin C

Information technology works for whatever triangle:

triangle

a, b and c are sides.

A, B and C are angles.

(Side a faces angle A,
side b faces bending B and
side c faces angle C).

And it says that:

When nosotros divide side a by the sine of angle A
information technology is equal to side b divided by the sine of angle B,
and likewise equal to side c divided by the sine of angle C

Certain ... ?

Well, let's do the calculations for a triangle I prepared earlier:

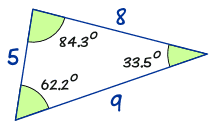5,8,9 Triangle

a sin A = eight sin(62.ii°) = 8 0.885... = 9.04...

b sin B = 5 sin(33.5°) = 5 0.552... = ix.06...

c sin C = ix sin(84.iii°) = ix 0.995... = 9.04...

The answers are almost the same!
(They would be exactly the aforementioned if we used perfect accuracy).

So now you lot can encounter that:

a sin A = b sin B = c sin C

Is This Magic?

triangle a b c

Not really, look at this general triangle and imagine it is two right-angled triangles sharing the side h:

The sine of an angle is the reverse divided by the hypotenuse, so:

triangle a b c

a sin(B) and b sin(A) both equal h, so we go:

a sin(B) = b sin(A)

Which can exist rearranged to:

a sin A = b sin B

We tin follow like steps to include c/sin(C)

How Do Nosotros Use It?

Let us meet an instance:

Example: Calculate side "c"

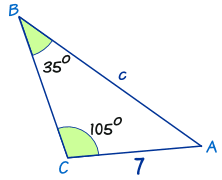
triangle 35 degrees, 105 degrees, 7

Law of Sines: a/sin A = b/sin B = c/sin C

Put in the values we know: a/sin A = 7/sin(35°) = c/sin(105°)

Ignore a/sin A (non useful to us): vii/sin(35°) = c/sin(105°)

At present we use our algebra skills to rearrange and solve:

Swap sides: c/sin(105°) = vii/sin(35°)

Multiply both sides by sin(105°): c = ( 7 / sin(35°) ) × sin(105°)

Calculate: c = ( seven / 0.574... ) × 0.966...

c = 11.viii (to ane decimal identify)

Finding an Unknown Bending

In the previous example we found an unknown side ...

... but we can besides utilise the Law of Sines to observe an unknown angle.

In this case it is best to turn the fractions upside down (sin A/a instead of a/sin A, etc):

sin A a = sin B b = sin C c

Example: Summate bending B

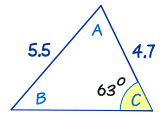
triangle 63 degrees, 4.7, 5.5

Outset with: sin A / a = sin B / b = sin C / c

Put in the values we know: sin A / a = sin B / 4.7 = sin(63°) / five.five

Ignore "sin A / a": sin B / 4.7 = sin(63°) / 5.five

Multiply both sides by four.7: sin B = (sin(63°)/5.v) × 4.7

Summate: sin B = 0.7614...

Inverse Sine: B = sin−ane(0.7614...)

B = 49.half dozen°

Sometimes At that place Are Two Answers !

There is ane very tricky thing we have to look out for:

Two possible answers.

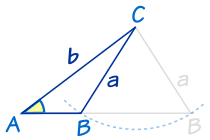Sine Law Ambiguous Case

Imagine we know bending A, and sides a and b.

Nosotros can swing side a to left or right and come up with 2 possible results (a small triangle and a much wider triangle)

Both answers are right!

This merely happens in the "Two Sides and an Angle not between" case, and even and so not always, only we take to lookout man out for it.

Only think "could I swing that side the other manner to also brand a correct answer?"

Instance: Calculate angle R

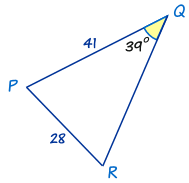
triangle 39 degrees, 41, 28

The kickoff affair to notice is that this triangle has different labels: PQR instead of ABC. Just that's OK. We only use P,Q and R instead of A, B and C in The Police force of Sines.

First with: sin R / r = sin Q / q

Put in the values we know: sin R / 41 = sin(39°)/28

Multiply both sides by 41: sin R = (sin(39°)/28) × 41

Calculate: sin R = 0.9215...

Inverse Sine: R = sin−1(0.9215...)

R = 67.ane°

But wait! There's some other angle that as well has a sine equal to 0.9215...

The calculator won't tell you this but sin(112.9°) is also equal to 0.9215...

So, how do we detect the value 112.9°?

Piece of cake ... take 67.1° abroad from 180°, like this:

180° − 67.ane° = 112.ix°

So there are two possible answers for R: 67.1° and 112.nine°:

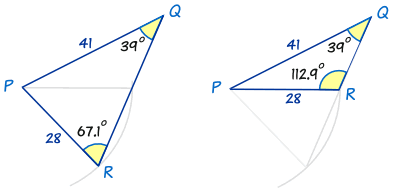
trig sine rule two angles example

Both are possible! Each one has the 39° bending, and sides of 41 and 28.

So, always check to see whether the alternative answer makes sense.

  • ... sometimes it will (similar higher up) and in that location are 2 solutions
  • ... sometimes it won't (meet below) and in that location is one solution
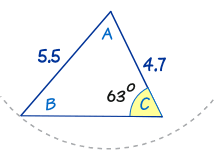trig sine rule one angle example

We looked at this triangle before.

As you can see, you lot tin try swinging the "five.5" line around, merely no other solution makes sense.

So this has only one solution.